matrixその①～事例紹介～

 

matrixの種類

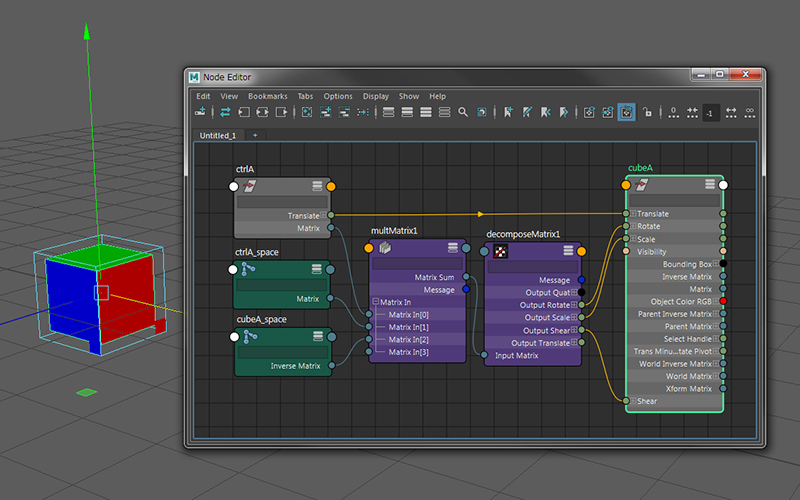
matrixには、matrix、inverseMatrix、parentMatrix、parentInverseMatrix、worldMatrix、worldInverseMatrixなどがあります。それぞれのmatrixを見て行きましょう。※心が折れそうな方は『matrix接続方法』まで飛ばして下さい。

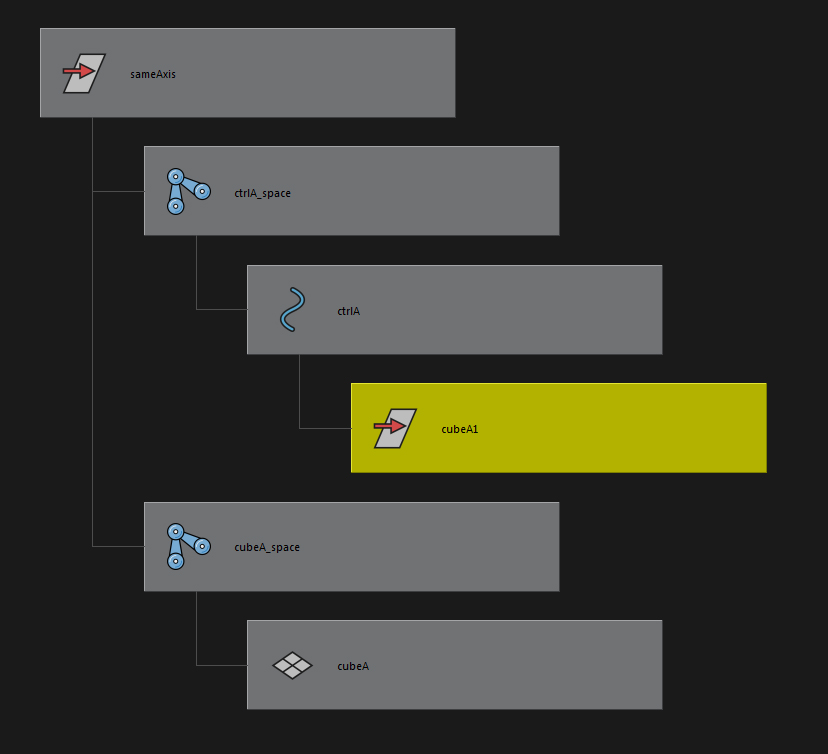
例えば、下図の階層の場合、

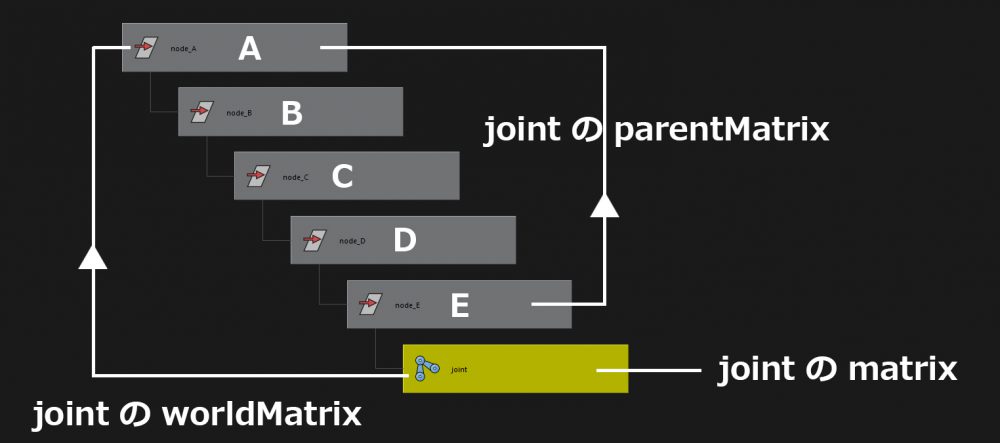
◆localMatrix
Joint自身のmatrixです。

 

◆parentMatrix
parentとは日本語で「親」。
すなわち、Joint の 親(E)までの階層（A～E）のmatrixを掛けた値です。
matrixを掛け算する際は、上の階層へ順番に上がって「matrix」を掛けていきます。
この場合の掛け算の順番は 「E.matrix」×「D.matrix」×「C.matrix」×「B.matrix」×「A.matrix」 となります。

 

◆worldMatrix
Jointまでの階層（A～EとJoint自身）のmatrixを掛けた値です。
matrixを掛け算する際は、上の階層へ順番に上がって「matrix」を掛けていきます。
この場合の掛け算の順番は 「Joint.matrix」×「E.matrix」×「D.matrix」×「C.matrix」×「B.matrix」×「A.matrix」  となります。
すなわち「Joint.matrix」×「joint.parentMatrix」と同じです。

 

InverseMatrixは上記の逆です。

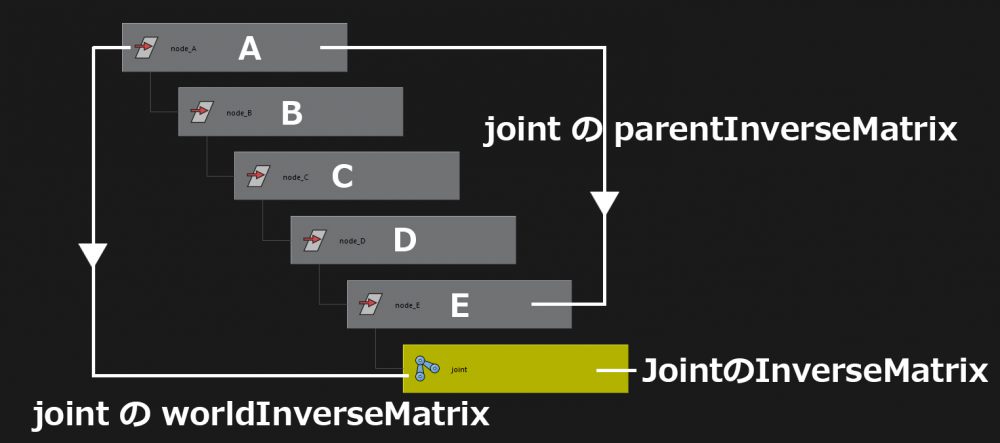
◆『localInverseMatrix』
Joint自身のinverseMatrix（逆Matrix）です。

 

◆『parentInverseMatrix』
Joint の 親(E)までの階層（A～E）のinverseMatrix（逆Matrix）を掛けた値です。
inverseMatrixを掛け算する際は、上の階層から順番に下がって「inverseMatrix」を掛けていきます。
この場合の掛け算の順番は「A.inverseMatrix」×「B.inverseMatrix」×「C.inverseMatrix」×「D.inverseMatrix」×「E.inverseMatrix」 となります。

 

◆『worldInverseMatrix』
Joint の 親(E)までの階層（A～E）とJoint自身のinverseMatrix（逆Matrix）を掛けた値です。
inverseMatrixを掛け算する際は、上の階層から順番に下がって「inverseMatrix」を掛けていきます。
この場合の掛け算の順番は「A.inverseMatrix」×「B.inverseMatrix」×「C.inverseMatrix」×「D.inverseMatrix」×「E.inverseMatrix」 × 「Joint.inverseMatrix」となります。
すなわち「Joint.parentInverseMatrix」×「joint.InverseMatrix」と同じです。 

 

matrixの接続方法

先ずはmatrixの使い方をご紹介します。
色んな試行錯誤を経てこの手法に辿り着きました。

少し泥臭い手法ですが、下記の通りに行えば、
どんな状況下であれ簡単にmatrixを繋ぐことができます。

詳細は後程ご説明しますが、手順は以下の通りです。

 

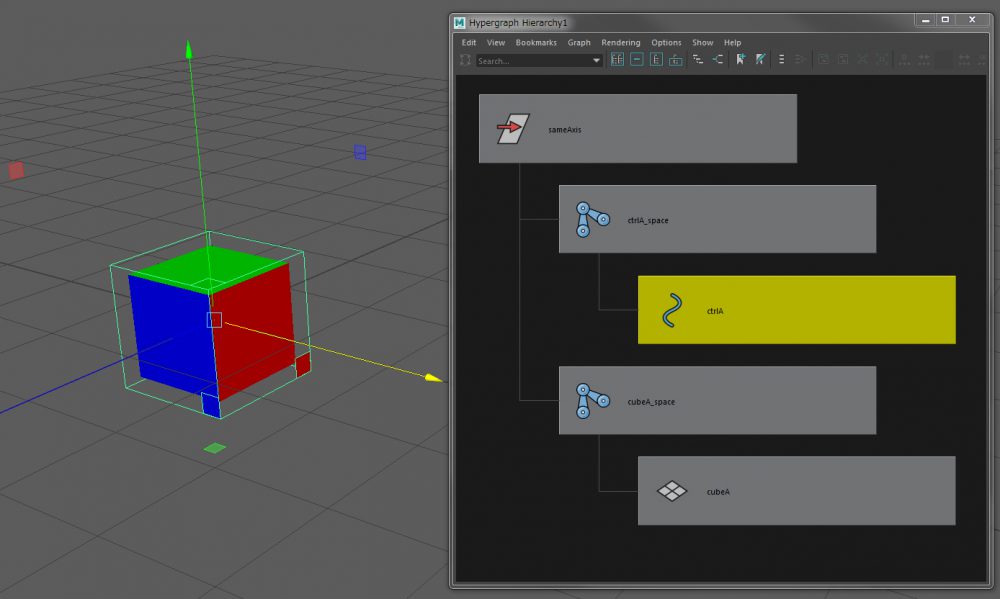
②制御される側のノードを複製します。
この場合、制御されるのはcubeAなのでcubeAを複製します。

 

③複製したcubeAを制御する側のノード、この場合ctrlAにペアレントします。

 

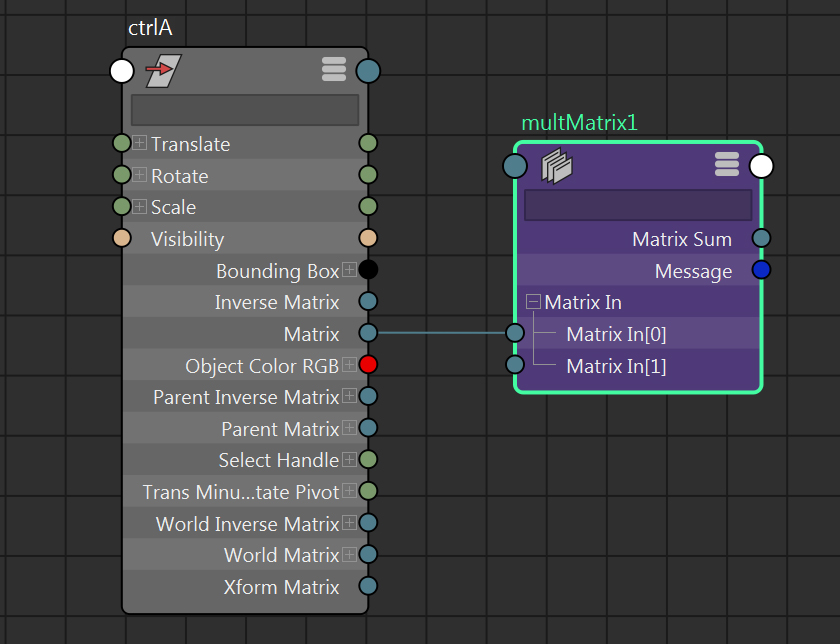
④複製したcubeA1のアトリビュートを確認すると、
制御する側であるctrlAと同じ位置と軸であるため、値に変化がありません。
値に変化が無い場合はmultMatrixへのsetAttrは不要です。

 

⑤次に、ctrlAとcubeAの共通の親を探しましょう。
どちらともsameAxisの階層内に格納されているので、共通の親はsameAxisとなります。
ctrlAからsameAxisまでの各ノードのmatrxをmultMatrixのmatrixIn[◎]に順番に接続します。
まず、ctrlAのmatrixをmultMatrixのmatrixIn[0]に接続します。

 

⑥次に、ctrlAの親のctrlA_spaceのmatrixをmultMatrixのmatrixIn[1]に接続します。

 

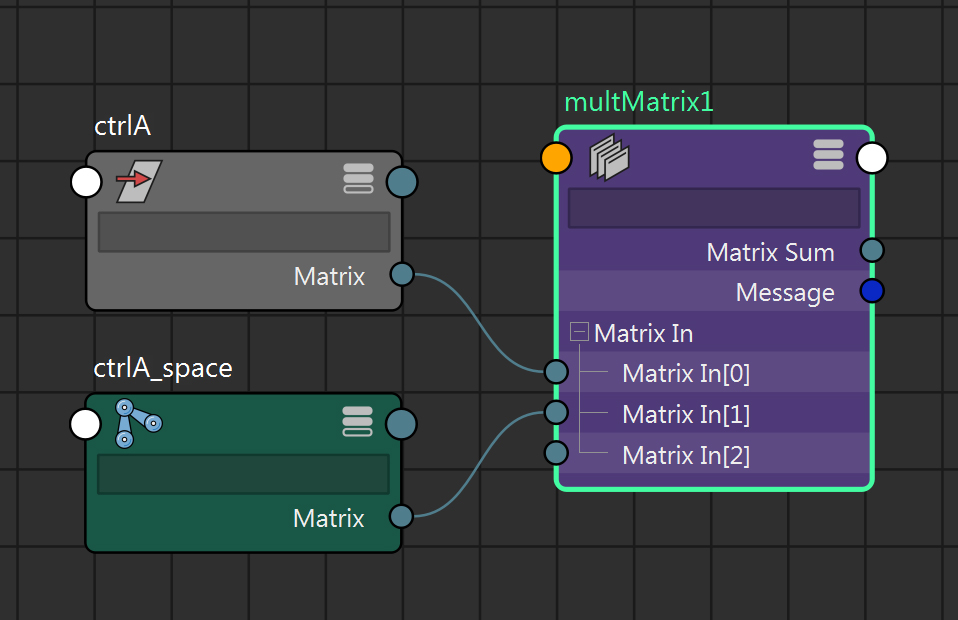
⑦共通の親（sameAxis）までのmatrixの接続が終わりました。
共通の親（sameAxis）の接続は飛ばして次はcubeAの親ノード（cubeA_space）まで接続します。
階層を下がる場合はinverseMatrixを接続します。
cubeA_spaceのinverseMatrixをmultMatrixのmatrixIn[2]に接続します。

 

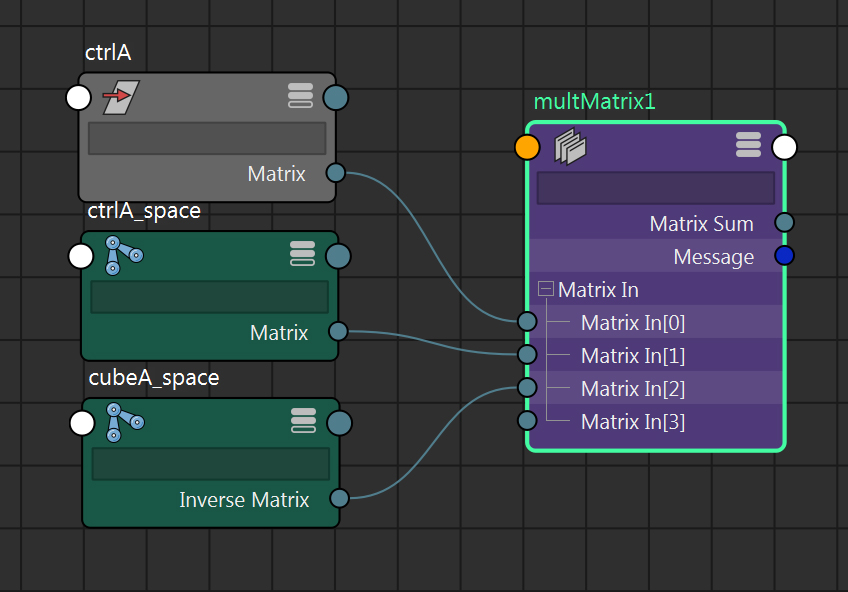
⑧後はこれらの結果をcubeAに接続するだけです。
NodeEditorでdecomposeMatrixノードを作成します。
※MatrixNodesプラグインをロードしていないと作成されません。
multMatrixのmatrixSumをdecomposeMatrixのinputMatrixに接続します。

 

⑨decomposeMatrixのoutputRotate、outputScale、outputShearをcubeAのrotate、scale、shearに接続します。

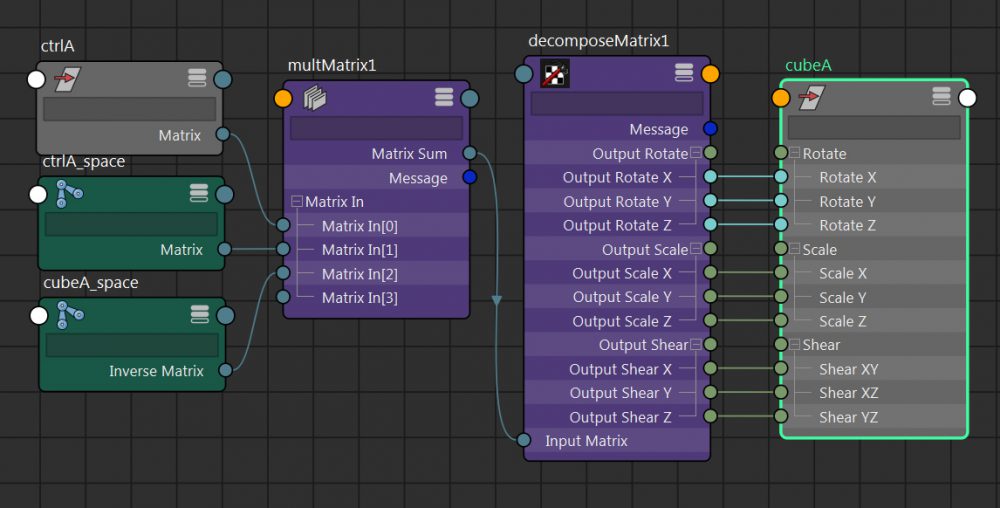
⑩ctrlAのtranslateとcubeAのtranslateを接続します。
※今回のケースでは、decomposeMatrixのoutputTranslateとcubeAのtranslateを接続しても構いません。
同じ結果になります。translateだけ別処理にする理由は後ほど。

 

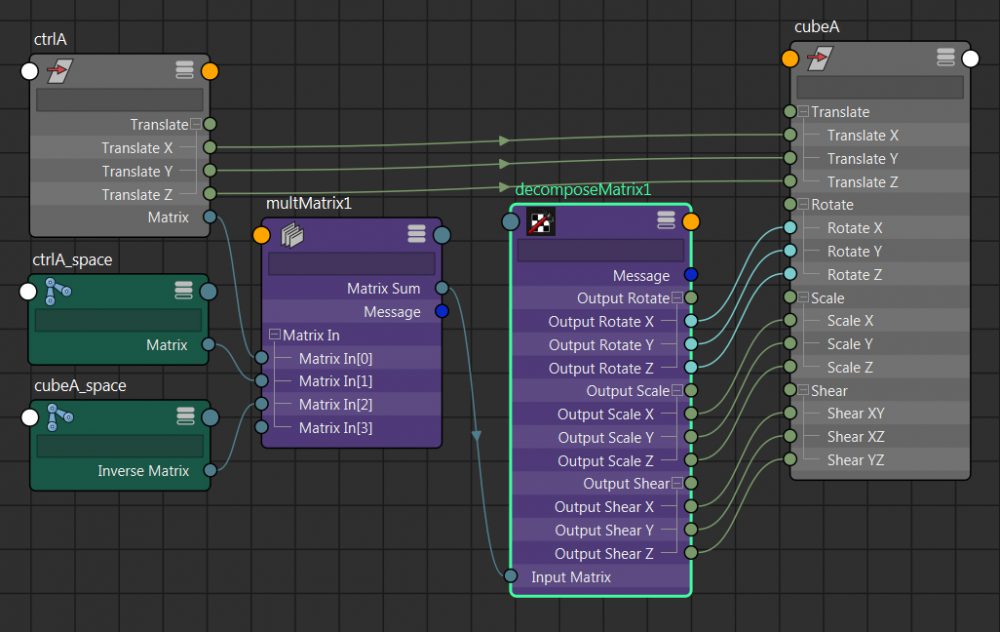
⑪完成です。
sameAxisノード階層内でのローカルmatrixを使用したコンストレインの出来上がりです！

 

まとめ

制御する側、される側の軸が違う場合もこの方法で対応できます。
つづく。